1. 01 背包
背包最大重量为4 物品为:
| 物品 | 重量 | 价值 |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
| 问背包能背的物品最大价值是多少? |
方法1: 动态规划
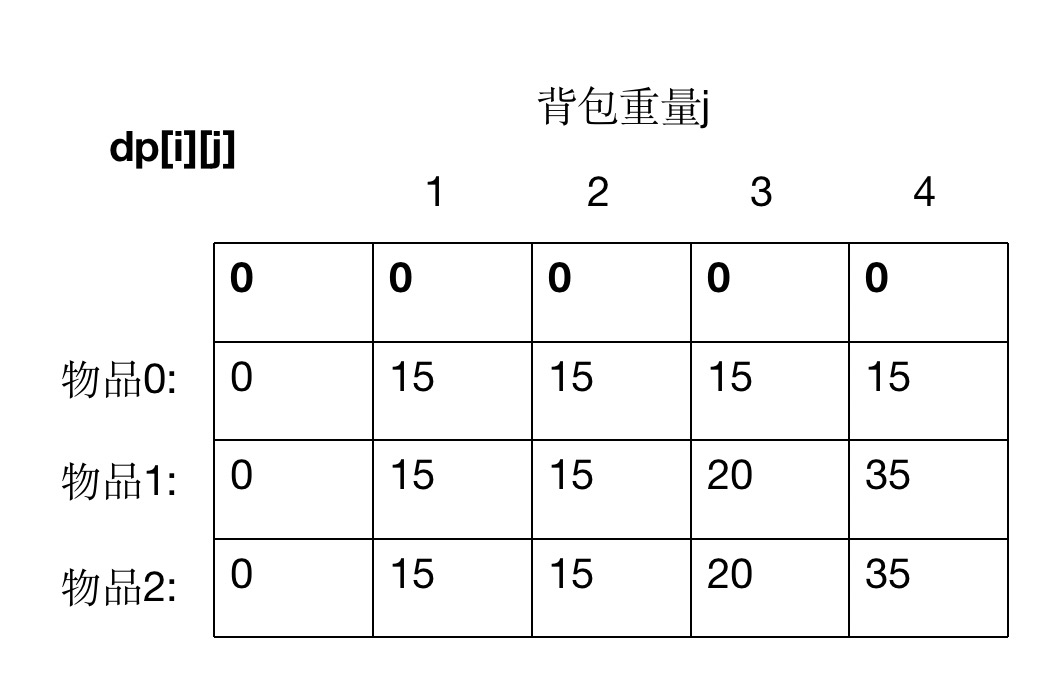
def knapsacks(W, N, weights, values):
dp = [[0 for _ in range(W+1)] for _ in range(N+1)]
for i in range(1, N+1):
weight = weights[i-1]
value = values[i-1]
for j in range(1, W+1):
if j<weight:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight]+value)
return dp[N][W]
2. 完全背包
0-1背包状态转移方程:
f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]
完全背包状态转移方程:
f[i][j]=max(f[i-1][j],f[i][j-w[i]]+v[i])
当不取的时候都是一样的最大价值等于f[i-1][j],等于i-1件物品在容量等于j的时候的最大值
当要取的时候这里有不同的地方
0-1背包是每一件物品只能选取一次 ,在解决0-1背包问题的时候我们需要找到f[i-1][j-w[i]最大价值。因为我们当前物品重量等于w[i],背包总容量等于j,我们就需要找到j-w[i]容量时第i-1件物品的时候最大价值然后加上我们这件物品的价值。 完全背包并不是找到上一件物品背包容量等于j-w[i]的时候,而是找到当前物品情况下j-w[i]的最大值,因为我们的物品可以无限制的使用,f[i][j-w[i]]+v[i]就是在求最大价值,是在放当前物品的时候容量等于j-w[i]的时候最大价值加上现在物品的价值,0-1背包是找到上一件物品背包容量等于j-w[i]的时候最大价值加上现在物品的价值,这就是0-1背包和完全背包不同的地方。
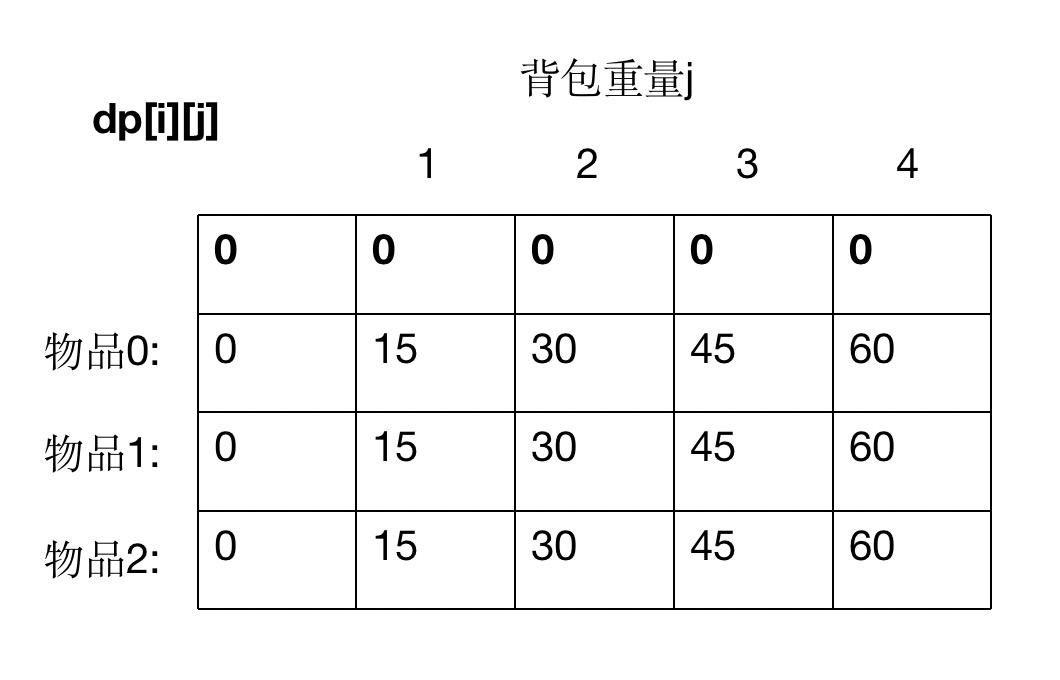
def knapsacks(W, N, weights, values):
dp = [[0 for _ in range(W+1)] for _ in range(N+1)]
for i in range(1, N+1):
weight = weights[i-1]
value = values[i-1]
for j in range(1, W+1):
if j<weight:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-weight]+value)
return dp[N][W]