import numpy as np
from matplotlib import pyplot as plt


# 生成权重以及偏执项layers_dim代表每层的神经元个数，
# 比如[2,3,1]代表一个三成的网络，输入为2层，中间为3层输出为1层
def init_parameters(layers_dim):
    L = len(layers_dim)
    parameters = {}
    for i in range(1, L):
        parameters["w" + str(i)] = np.random.random([layers_dim[i], layers_dim[i - 1]])
        parameters["b" + str(i)] = np.zeros((layers_dim[i], 1))
    return parameters


def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))


# sigmoid的导函数
def sigmoid_prime(z):
    return sigmoid(z) * (1 - sigmoid(z))


# 前向传播，需要用到一个输入x以及所有的权重以及偏执项，都在parameters这个字典里面存储
# 最后返回会返回一个caches里面包含的 是各层的a和z，a[layers]就是最终的输出
def forward(x, parameters):
    a = []
    z = []
    caches = {}
    a.append(x)
    z.append(x)
    layers = len(parameters) // 2
    # 前面都要用sigmoid
    for i in range(1, layers):
        z_temp = parameters["w" + str(i)].dot(x) + parameters["b" + str(i)]
        z.append(z_temp)
        a.append(sigmoid(z_temp))
    # 最后一层不用sigmoid
    z_temp = parameters["w" + str(layers)].dot(a[layers - 1]) + parameters["b" + str(layers)]
    z.append(z_temp)
    a.append(z_temp)

    caches["z"] = z
    caches["a"] = a
    return caches, a[layers]


# 反向传播，parameters里面存储的是所有的各层的权重以及偏执，caches里面存储各层的a和z
# al是经过反向传播后最后一层的输出，y代表真实值
# 返回的grades代表着误差对所有的w以及b的导数
def backward(parameters, caches, al, y):
    layers = len(parameters) // 2
    grades = {}
    m = y.shape[1]
    # 假设最后一层不经历激活函数
    # 就是按照上面的图片中的公式写的
    grades["dz" + str(layers)] = al - y
    grades["dw" + str(layers)] = grades["dz" + str(layers)].dot(caches["a"][layers - 1].T) / m
    grades["db" + str(layers)] = np.sum(grades["dz" + str(layers)], axis=1, keepdims=True) / m
    # 前面全部都是sigmoid激活
    for i in reversed(range(1, layers)):
        grades["dz" + str(i)] = parameters["w" + str(i + 1)].T.dot(grades["dz" + str(i + 1)]) * sigmoid_prime(
            caches["z"][i])
        grades["dw" + str(i)] = grades["dz" + str(i)].dot(caches["a"][i - 1].T) / m
        grades["db" + str(i)] = np.sum(grades["dz" + str(i)], axis=1, keepdims=True) / m
    return grades


# 就是把其所有的权重以及偏执都更新一下
def update_grades(parameters, grades, learning_rate):
    layers = len(parameters) // 2
    for i in range(1, layers + 1):
        parameters["w" + str(i)] -= learning_rate * grades["dw" + str(i)]
        parameters["b" + str(i)] -= learning_rate * grades["db" + str(i)]
    return parameters


# 计算误差值
def compute_loss(al, y):
    return np.mean(np.square(al - y))


# 加载数据
def load_data():
    """
    加载数据集
    """
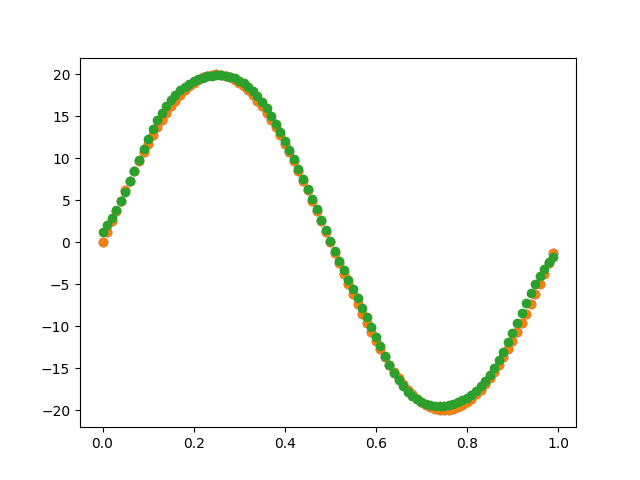
    x = np.arange(0.0, 1.0, 0.01)
    y = 20 * np.sin(2 * np.pi * x)
    # 数据可视化
    plt.scatter(x, y)
    return x, y


# 进行测试
x, y = load_data()
x = x.reshape(1, 100)
y = y.reshape(1, 100)
plt.scatter(x, y)
parameters = init_parameters([1, 25, 1])
al = 0
for i in range(4000):
    caches, al = forward(x, parameters)
    grades = backward(parameters, caches, al, y)
    parameters = update_grades(parameters, grades, learning_rate=0.3)
    if i % 100 == 0:
        print(compute_loss(al, y))
plt.scatter(x, al)
plt.show()