1 数据说明
2 结果展示
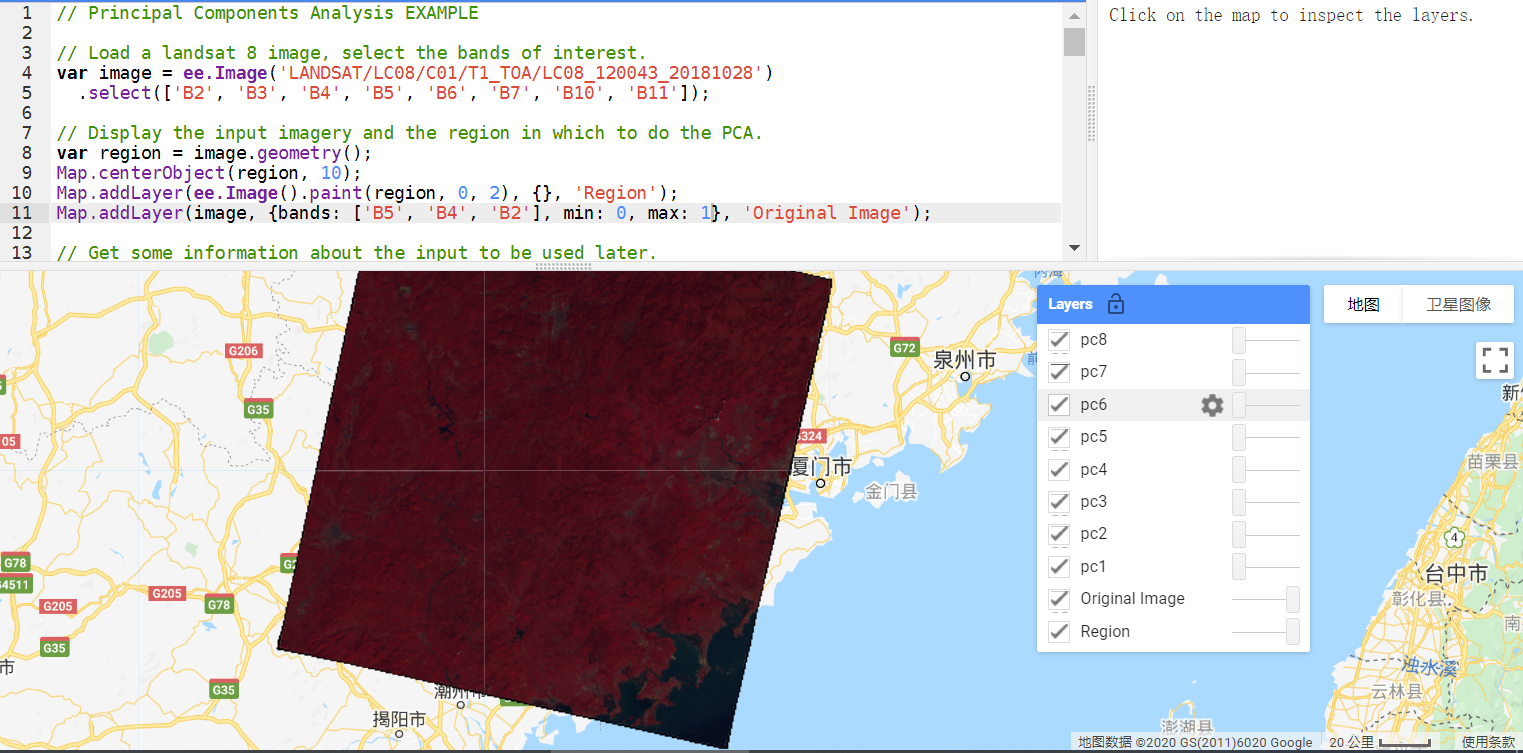
3 详细代码
// Principal Components Analysis EXAMPLE
// Load a landsat 8 image, select the bands of interest.
var image = ee.Image('LANDSAT/LC8_L1T/LC80440342014077LGN00')
.select(['B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B10', 'B11']);
// Display the input imagery and the region in which to do the PCA.
var region = image.geometry();
Map.centerObject(region, 10);
Map.addLayer(ee.Image().paint(region, 0, 2), {}, 'Region');
Map.addLayer(image, {bands: ['B5', 'B4', 'B2'], min: 0, max: 20000}, 'Original Image');
// Get some information about the input to be used later.
var scale = image.projection().nominalScale();
var bandNames = image.bandNames();
// Mean center the data to enable a faster covariance reducer
// and an SD stretch of the principal components.
var meanDict = image.reduceRegion({
reducer: ee.Reducer.mean(),
geometry: region,
scale: scale,
maxPixels: 1e9
});
var means = ee.Image.constant(meanDict.values(bandNames));
var centered = image.subtract(means);
// This helper function returns a list of new band names.
var getNewBandNames = function(prefix) {
var seq = ee.List.sequence(1, bandNames.length());
return seq.map(function(b) {
return ee.String(prefix).cat(ee.Number(b).int());
});
};
// This function accepts mean centered imagery, a scale and
// a region in which to perform the analysis. It returns the
// Principal Components (PC) in the region as a new image.
// [START principal_components]
var getPrincipalComponents = function(centered, scale, region) {
// Collapse the bands of the image into a 1D array per pixel.
var arrays = centered.toArray();
// Compute the covariance of the bands within the region.
var covar = arrays.reduceRegion({
reducer: ee.Reducer.centeredCovariance(),
geometry: region,
scale: scale,
maxPixels: 1e9
});
// Get the 'array' covariance result and cast to an array.
// This represents the band-to-band covariance within the region.
var covarArray = ee.Array(covar.get('array'));
// Perform an eigen analysis and slice apart the values and vectors.
var eigens = covarArray.eigen();
// This is a P-length vector of Eigenvalues.
var eigenValues = eigens.slice(1, 0, 1);
// This is a PxP matrix with eigenvectors in rows.
var eigenVectors = eigens.slice(1, 1);
// Convert the array image to 2D arrays for matrix computations.
var arrayImage = arrays.toArray(1);
// Left multiply the image array by the matrix of eigenvectors.
var principalComponents = ee.Image(eigenVectors).matrixMultiply(arrayImage);
// Turn the square roots of the Eigenvalues into a P-band image.
var sdImage = ee.Image(eigenValues.sqrt())
.arrayProject([0]).arrayFlatten([getNewBandNames('sd')]);
// Turn the PCs into a P-band image, normalized by SD.
return principalComponents
// Throw out an an unneeded dimension, [[]] -> [].
.arrayProject([0])
// Make the one band array image a multi-band image, [] -> image.
.arrayFlatten([getNewBandNames('pc')])
// Normalize the PCs by their SDs.
.divide(sdImage);
};
// [END principal_components]
// Get the PCs at the specified scale and in the specified region
var pcImage = getPrincipalComponents(centered, scale, region);
// Plot each PC as a new layer
for (var i=0; i<bandNames.length().getInfo(); i++) {
var band = pcImage.bandNames().get(i).getInfo();
Map.addLayer(pcImage.select([band]), {min:-2, max:2}, band);
}
