# from hydra.utils.gpu_usage import limit_gpu_memory
# limit_gpu_memory(int(2) * 1024, 1)

import pandas as pd
import numpy as np
import jieba
import gensim
from keras.preprocessing.text import Tokenizer, text_to_word_sequence
from keras.preprocessing.sequence import pad_sequences
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
df_train = pd.read_csv("./data/siamese/df_train.txt",sep="\\t", header=None,engine='python')
df_test = pd.read_csv("./data/siamese/df_test.txt",sep="\\t", header=None,engine='python')
df =  df_train.append(df_test)
sent1 = [ list(i) for i in df[0].tolist()]
sent2 = [ list(i) for i in df[1].tolist()]
tokenizer = Tokenizer(num_words=None,lower=False, char_level=True, split="")
tokenizer.fit_on_texts(sent1+sent2)
word_dict = tokenizer.word_index
word_num = len(word_dict)+1
max_length = max(len(i) for i in sent1+sent2)
word_num, max_length
x1 = tokenizer.texts_to_sequences(sent1)
x2 = tokenizer.texts_to_sequences(sent2)
x1 = pad_sequences(x1, maxlen=max_length, value=0,truncating='post',padding='post')
x2 = pad_sequences(x2, maxlen=max_length, value=0,truncating='post',padding='post')
y = df[[2]].to_numpy()
train_x1 = x1[:len(df_train),:]
train_x2 = x2[:len(df_train),:]
train_y = y[:len(df_train),:]

test_x1 = x1[len(df_train):,:]
test_x2 = x2[len(df_train):,:]
test_y = y[len(df_train):,:]
print(train_x1.shape, train_x2.shape, train_y.shape)
print(test_x1.shape, test_x2.shape, test_y.shape)

emb_path = "./data/siamese/token_vec_300.bin"
word_dim = 300
embedding_dict = gensim.models.KeyedVectors.load_word2vec_format(emb_path, binary=False)

embedding_matrix = np.zeros((word_num, word_dim))
for word, i in word_dict.items():
    if word in embedding_dict.vocab:
        embedding_matrix[i] = embedding_dict[word]

from keras.utils import plot_model
from keras import backend as K
from keras.preprocessing.sequence import pad_sequences
from keras.models import Model, load_model
from keras.layers import Input, Embedding, LSTM, Dropout, Lambda, Bidirectional

'''基于曼哈顿空间距离计算两个字符串语义空间表示相似度计算'''
def exponent_neg_manhattan_distance(inputX):
    (sent_left, sent_right) = inputX
    return K.exp(-K.sum(K.abs(sent_left - sent_right), axis=1, keepdims=True))

'''基于欧式距离的字符串相似度计算'''
def euclidean_distance(inputX):
    (sent_left, sent_right) = inputX
    sum_square = K.sum(K.square(sent_left - sent_right), axis=1, keepdims=True)
    return K.sqrt(K.maximum(sum_square, K.epsilon()))

'''共享权重的share model'''
def create_base_network(input_shape):
    inputs = Input(shape=input_shape)
    lstm1 = Bidirectional(LSTM(128, return_sequences=True))(inputs)
    lstm1 = Dropout(0.5)(lstm1)
    lstm2 = Bidirectional(LSTM(32))(lstm1)
    lstm2 = Dropout(0.5)(lstm2)
    mode = Model(inputs=inputs, outputs=lstm2)
    return mode

embedding_layer = Embedding(input_dim = word_num,
                            output_dim = word_dim,
                            weights=[embedding_matrix],
                            input_length=max_length,
                            trainable= False,
                            mask_zero=True)

left_input = Input(shape=(max_length,))
right_input = Input(shape=(max_length,))

encoded_left = embedding_layer(left_input)
encoded_right = embedding_layer(right_input)

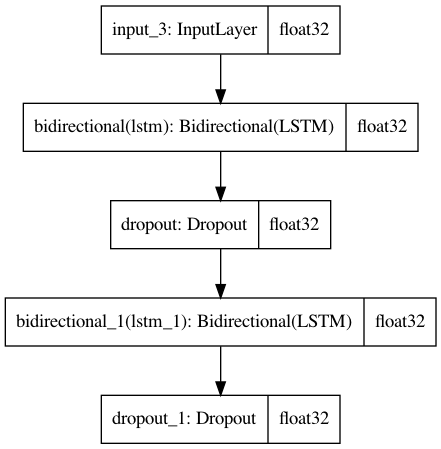
shared_lstm = create_base_network(input_shape=(max_length,word_dim)) # 最后真正使用的编码模型
left_output = shared_lstm(encoded_left)
right_output = shared_lstm(encoded_right)
distance = Lambda(exponent_neg_manhattan_distance)([left_output, right_output])
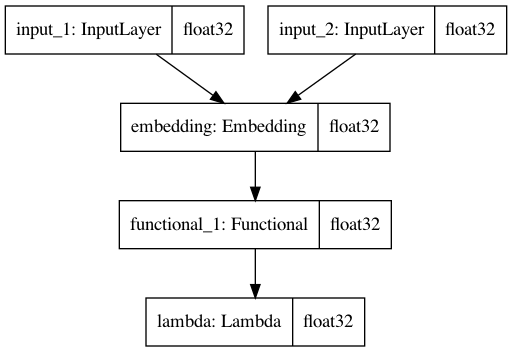
model = Model(inputs = [left_input, right_input], outputs = distance) # 训练时使用的模型
model.compile(loss='binary_crossentropy', optimizer='nadam', metrics=['accuracy'])
model.summary()
plot_model(model,to_file='model.png',show_shapes=True,show_dtype=True)

plot_model(shared_lstm,to_file='shared_lstm.png',show_shapes=True,show_dtype=True)