牛客网-NC45 实现二叉树先序，中序和后序遍历

评论
1014 views

给定一棵二叉树，分别按照二叉树先序，中序和后序打印所有的节点。

数据范围：0 <n≤1000，树上每个节点的val值满足: 0<val≤100

要求：空间复杂度 O(n)，时间复杂度 O(n)

样例解释：

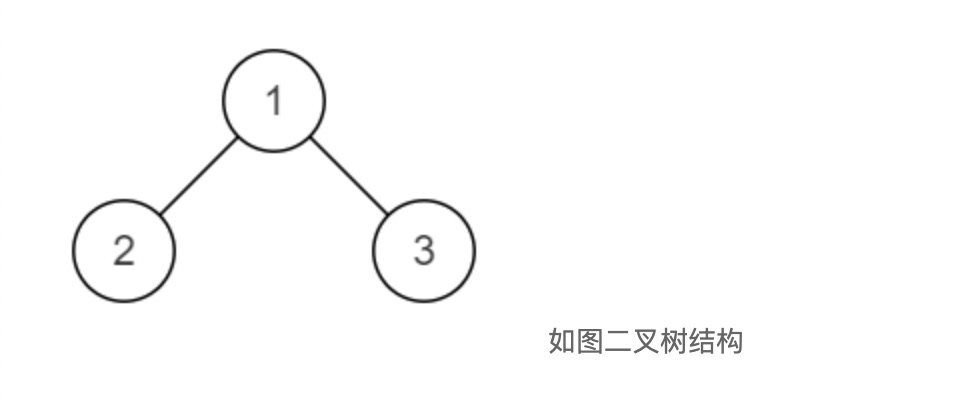
示例1

输入：
{1,2,3}
返回值：
[[1,2,3],[2,1,3],[2,3,1]]

示例2

输入：
{}
返回值：
[[],[],[]]

备注：

n < 10^6

方法1：递归

class Solution:
    def threeOrders(self , root: TreeNode) -> List[List[int]]:
        # write code here
        pre_res = []
        def preprint(root):
            if root!=None:
                pre_res.append(root.val)
                preprint(root.left)
                preprint(root.right)
            return pre_res
        mid_res = []
        def midprint(root):
            if root != None:
                midprint(root.left)
                mid_res.append(root.val)
                midprint(root.right)
            return mid_res
        end_res = []
        def endprint(root):
            if root != None:
                endprint(root.left)
                endprint(root.right)
                end_res.append(root.val)
            return end_res

        res = []
        res.append(preprint(root))
        res.append(midprint(root))
        res.append(endprint(root))
        return res

方法2: 迭代

其核心思想如下：

  • 使用颜色标记节点的状态，新节点为白色，已访问的节点为灰色。
  • 如果遇到的节点为白色，则将其标记为灰色，然后将其右子节点、自身、左子节点依次入栈。
  • 如果遇到的节点为灰色，则将节点的值输出。
  • 以上总结为：新白已灰；遇白标灰，右自左依入栈；遇灰值出。
class Solution:
    def threeOrders(self , root: TreeNode) -> List[List[int]]:
        # write code here
        res = []
        res.append(self.preprint(root))
        res.append(self.midprint(root))
        res.append(self.endprint(root))
        return res

    def preprint(self,root):
        res = []
        if root==None:return res
        white, gray = 0,1
        q = [(white, root)]
        while q:
            color, node = q.pop(-1)
            if node is None: continue
            if color==white:
                q.append((white, node.right))
                q.append((white, node.left))
                q.append((gray, node))
            else:
                res.append(node.val)
        return res

    def midprint(self,root):
        res = []
        if root==None:return res
        white, gray = 0,1
        q = [(white, root)]
        while q:
            color, node = q.pop(-1)
            if node is None: continue
            if color==white:
                q.append((white, node.right))
                q.append((gray, node))
                q.append((white, node.left))
            else:
                res.append(node.val)
        return res

    def endprint(self,root):
        res = []
        if root==None:return res
        white, gray = 0,1
        q = [(white, root)]
        while q:
            color, node = q.pop(-1)
            if node is None: continue
            if color==white:
                q.append((gray, node))
                q.append((white, node.right))
                q.append((white, node.left))
            else:
                res.append(node.val)
        return res